HB's Blog HomeArchivesTagsCategoriesGallery
初探动态规划算法
|Algorithm
Word count: 2.8k|Reading time: 10 min

概念

维基百科的定义如下：

dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

从中我们知道动态规划关注三点：

  1. 把一个问题划分为若干相似的子问题
  2. 所有的子问题只需要解决一次
  3. 存储子问题的解

动态规划所涉及的几个重要概念也如下所示：

  1. 最优子结构：每个阶段的最优状态可以从之前某个阶段的某个或某些状态得到。即思考大问题的最优解是如何由小问题的最优解得到的。
  2. 无后效性：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受此阶段以前各段状态的影响 - “未来和过去无关”
  3. 边界：通常是问题的结束条件
  4. 状态转移公式：说明了问题的每一阶段与上一个/一些阶段的相互关系
  5. 子问题重叠性质：在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法对此进行了优化，对每个子问题只需要计算一次，把计算结果存储在表格中，便于下次使用

算法设计

一个动态规划算法基本可以分为以下步骤：

  1. 从题目中确定最优子结构是什么
  2. 确定问题的边界条件
  3. 根据上述两步构建数学模型，得到相应的状态转移方程
  4. 根据数学模型进行代码编写

例题一

有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

解析

假设0-9级台阶共有X个走法，0-8级台阶共有Y个走法，则总共的走法共有X+Y个走法，如下图所示：

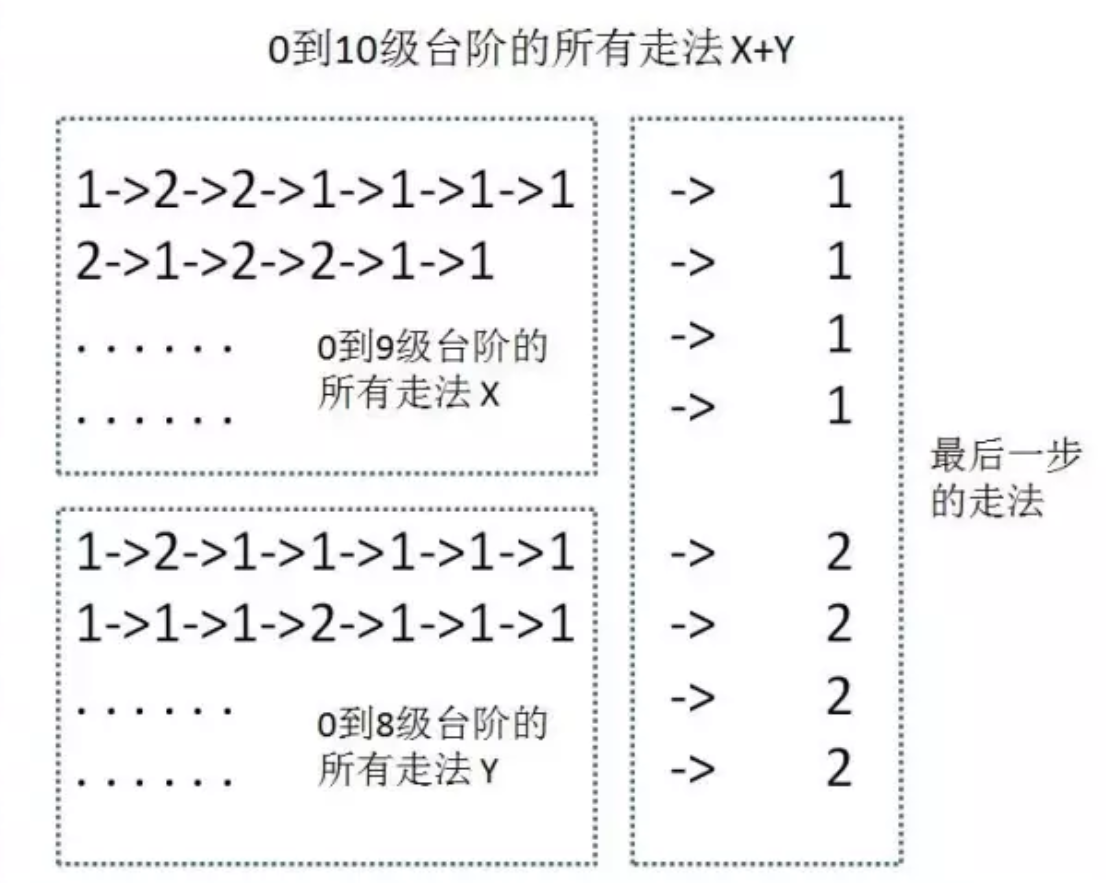
对于8级台阶到10台阶，只存在跨越2步这个可能，因为若到了8级台阶之后，每次跨越1步，就到了9级台阶，此种走法包含到了9级台阶的X走法之中。
综上可知，到9级台阶的所有走法由到第8级台阶和第7级台阶组成….，以此类推。
无后效性体现在8级台阶之后的所有走法不受以前各级走法的影响。

数学建模

使用数学公式可表示为 F (10) = F (9) + F (8) ，其可以看作为最优子结构，则以此类推 F (9) = F (8) + F (7)…, 从而可以得到如下公式：
  F (1) = 1;
  F (2) = 2;
  F (n) = F (n-1) + F (n-2);
从上面的公式可以看出 F (1) = 1，F (2) = 2 称为问题的边界，若一个问题没有边界，则永远无法得到有限的结果，F (n) = F (n-1) + F (n-2) 是状态转移方程，说明了问题的每一阶段与上一个/一些阶段的相互关系。

代码实现

1. 递归实现

int getClimbingWays(int n){
        if (n < 1){
            return 0;
        }
        if (n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }
        return getClimbingWays(n-1) + getClimbingWays(n - 2);
    }

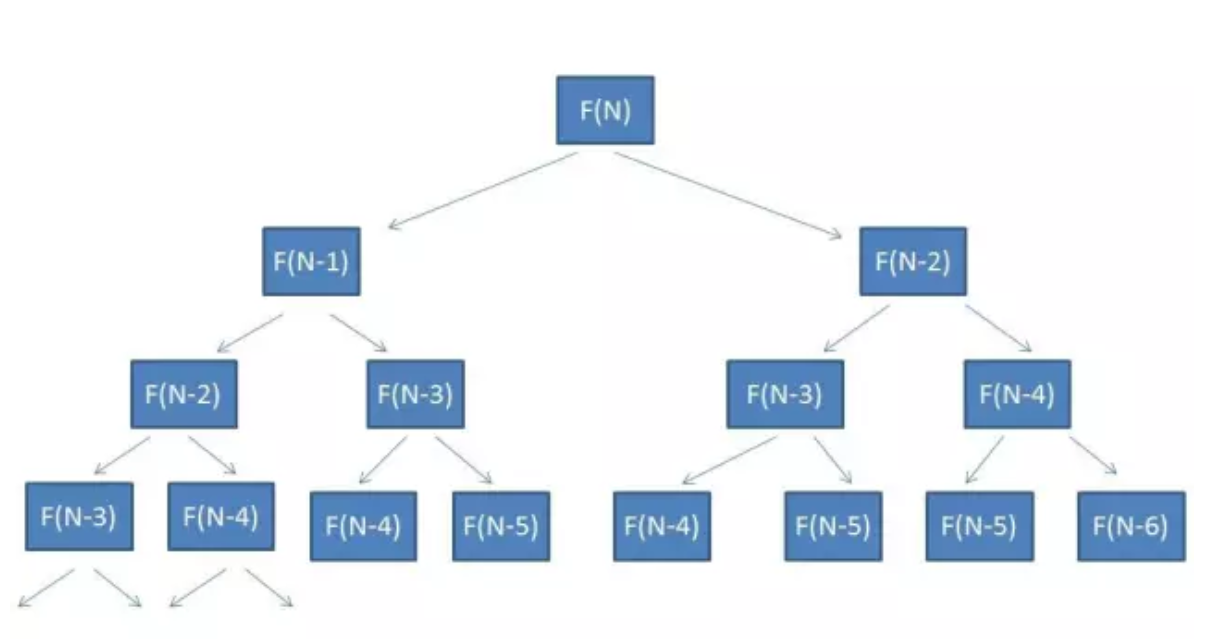
如下图递归的次数类似形成如下二叉树，每个节点表示递归方法所计算的次数，二叉树高度为N-1，节点个数接近2的N-1次方个，随递归方法的时间复杂度为O(N^2)。

2. 备忘录算法

使用递归算法有大量的重复计算，就像下图所示，

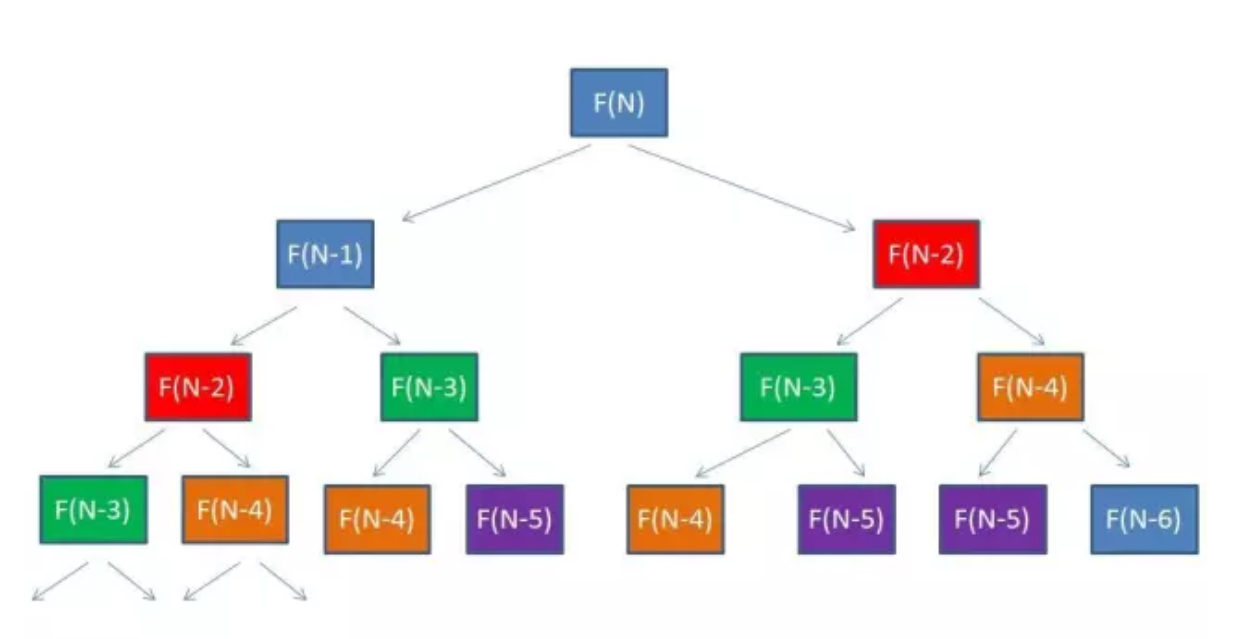
int getClimbingWays(int n, HashMap<Integer, Integer> memo){
        if (n < 1){
            return 0;
        }
        if (n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }
        if (memo.containsKey(n)){
            return memo.get(n);
        }else {
            int value =  getClimbingWays(n -1,memo) + getClimbingWays(n -2, memo);
            memo.put(n,value);
            return value;
        }
    }

此时的时间和空间复杂度都为O(N)

3. 动态规划算法

就算备忘录算法对算法进行了优化，但是其还是要保持所有的子状态，造成空间复杂度过高，并且递归算法和备忘录算法都是自顶向下进行处理，即从 F (N) 慢慢迭代到 F (1) 和 F (2) ，现尝试自底向上进行求解，只保存当前状态的前两个状态。分析过程如下：

  1. F (1)和F (2)为已知道结果，第一次迭代后，台阶数为3，走法数量为3，可知 F (3) 只依赖 F (2) 和 F (2)，可得下表

  2. 第二次迭代后，台阶数为4，走法为5，可知 F (4) 只依赖于 F (3) 和 F (2)

其他迭代也如上所示，可知在每次迭代过程中，只需要保存前两个状态即可。

static int getClimbingWays(int n){
        if (n < 1){
            return 0;
        }
        if(n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }
        int a = 1;
        int b = 2;
        int ResultWays = 0;
        for (int i = 3; i <= n; i++){
            ResultWays = a + b;
            a = b;
            b = ResultWays;
        }
        return ResultWays;
    }

动态规划算法的时间复杂度为O(N)，空间复杂度为O(1)。

例题二

有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？
其中金矿1：400金/5人，金矿2：500金/5人，金矿3：200金/3人，金矿4：300金/4人，金矿5：350金/3人

解析

我们的最终要求解的问题是：10人5金矿时的最优选择，我们可以先假设最优子结构为10个人4个金矿挖出最多黄金，但是第五个金矿存在挖或者不挖的可能性，遂可进行扩展分为两个最优子结构：

  1. 第五个金矿不挖，最优子结构为10个人4个金矿挖出最多黄金
  2. 第五个金矿挖，最优子结构为10 - 第五个金矿所需人数时挖4个金矿的最优选择 + 第五个金矿的黄金储量

则五个金矿的最优选择就是（10个人4个金矿的最优选择）和（10 - 第五个金矿所需人数时挖4个金矿的最优选择 + 第五个金矿的黄金储量）的最大值。
边界分为两种情况，说明如下：

  1. 只有一个金矿，并且工人数满足金矿所需人数要求，遂得到黄金数量为第
    一个金矿的储量
  2. 只有一个金矿，若工人数不满足金矿所需人数要求，则得到的黄金数量为0

数学建模

金矿数量 = N ，工人数量 = W ，金矿黄金量 G [] ，每个金矿的用工数量 P [] 。数组下标都从0开始，则5座金矿和4座金矿的最优选择之间存在如下关系： F (5,10) = MAX (F (4,10), F (4,10-P [4]) +G (4) ) 。可以得到如下状态转移方程：
  F (N W ) =0 (N <= 1, W < P [0]) ; // 金矿数量小于1或一个金矿但是人数不足
  F (N,W ) = G [0] (N == 1, W >= P [0]) ; // 金矿数量为1个，需要挖矿人数符合
  F (N,W ) = F (N-1, W) (N > 1, W < P [N-1]) ; //金矿数量大于一个，但是剩余的挖矿人数已经不满足继续挖矿
  F (N,W ) = MAX (F (N-1,W ), F (N-1,W-P [N-1]) +G (N -1) ) ; //金矿数量大于一个，剩余的挖矿人数满足继续挖矿要求

代码实现

1. 递归实现

public static int getMostGold(int n, int w, int g[], int p[]){
        if (n == 1){
            return w < p[n-1] ? 0 : g[n-1];
        }
        if (w < p[n - 1]){
            return getMostGold(n-1,w,g,p);
        }
        return Math.max(getMostGold(n-1,w,g,p), getMostGold(n-1, w - p[n-1],g,p) + g[n-1]);
    }

递归实现的时间复杂度为O(2^N)。

2. 动态规划实现

给出一个表格，表格的列表示金矿（ N ），行表示工人数（ W ），相对应的值给定 N 和 W 之后获得的黄金数量。

  1. 得到第一行数据如下：

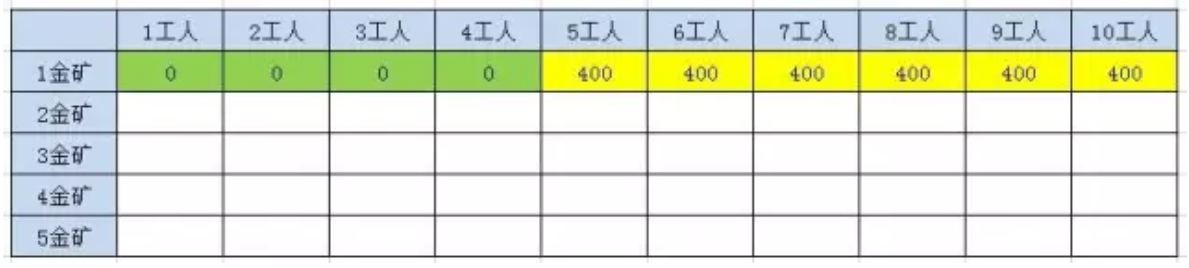
  2. 当工人数在5-9期间时，设 S =5~9，F (2, S ) = MAX (F (1, S ), F (1, S -5) +500) , 其中都因为 S -5 < 5 ，则5~9格子中，黄金量为500。而当 _W = 10 _时，F (2, 10) = MAX (F (1, 10), F (1, 5) + 500) 为900。

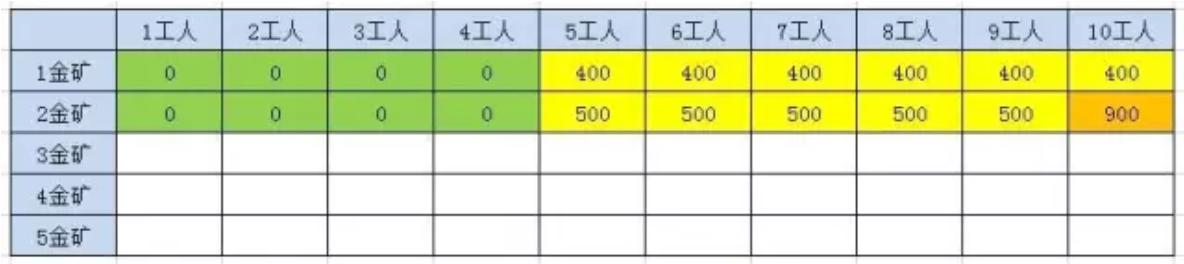
  3. 第三个金矿200储量，需要3人，第四金矿300储量，需要4人，第五金矿350
    储量，需要3人，依次计算可得下表：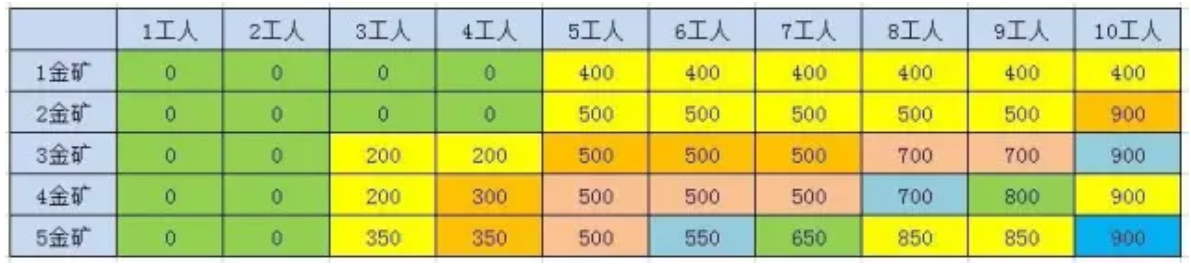

综上可得出规律，每个格子的黄金量都是都前一行的一个或者两个格子推导而来，例如3金矿8工人时，就来自于2金矿5工人+第三个金矿储量和2金矿8工人，即MAX (F (2, 8 ), F (2, 5) +200) = MAX (500, 200 + 500) = 700。所以我们只需要存储前一行的数据，就可以推导出新的一行。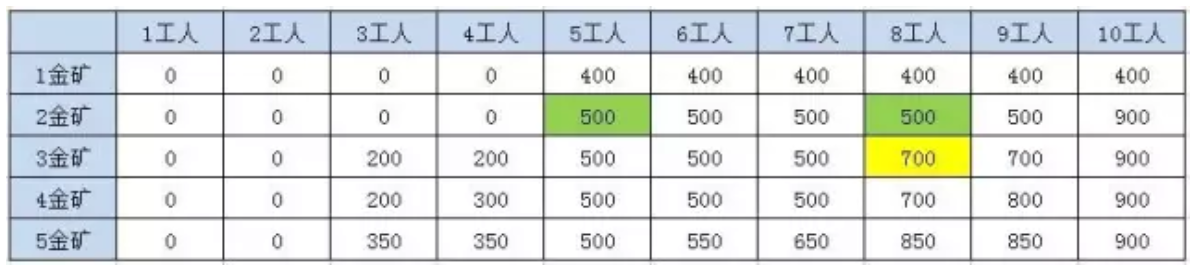

public void getMostGold(int n, int w, int[] g, int[] p){
        int[] preResult = new int [w]; // 保存前一行结果
        int[] results = new int [w];  // 保存当前结果
        // 填充第一个金矿的数据
        for (int i = 0; i < w; i++){
            if (i+1 < p[0]){
                preResult[i] = 0;  // 对应数学模型 F(N W)=0 (N<=1,W<P[0]);
            }else {
                preResult[i] = g[0];  // 对应数学模型 F(N,W)=G[0] (N==1,W>=P[0]);
            }
        }
        showResults(preResult);  // 展示第一行的数据
   
        //对其他金矿进行处理，从第二个金矿开始,外层循环时金矿数量，内层循环时工人数
        for (int i = 1; i < n; i++){   
            for (int j = 0; j < w; j++){
                if (j + 1 < p[i]){
                    results[j] = preResult[j]; // 对应数学模型 F(N,W)=F(N-1,W) (N>1,W<P[N-1]);
                }else if (j + 1 == p[i]){
                    results[j] = Math.max(preResult[j],0 + g[i]); // 特殊情况,拥有工人数刚好与要挖的下一个金矿的所需工人数相同 若要挖下一个金矿，则挖前一个金矿的人数为0
                }else {
                    results[j] = Math.max(preResult[j],preResult[j - p[i]] + g[i]); // 对应数学模型 F(N,W)=MAX(F(N-1,W),F(N-1,W-P[N-1]+G(N-1));
                }
            }
            showResults(results);
            preResult = results.clone();
            // preResult = results; 不可直接进行引用的赋值
        }
    }
public void showResults(int[] results){
        for(int i:results){
            System.out.print(i+" ");
        }
        System.out.println();
}

动态规划实现的时间复杂度为O(N*W)，空间复杂度为O(W)。

总结

但是动态规划算法在有些情况下不一定是最好的选择，当5个金矿1000个工人时，因为动态规划的时间和空间复杂度与W成正比，而递归算法与W无关，其时间和空间复杂度都不如递归算法来的好。

参考资料

[1]. https://mp.weixin.qq.com/s/3h9iqU4rdH3EIy5m6AzXsg
[2]. https://www.zhihu.com/question/23995189

Author: HB
Link: http://www.huangbin.fun/初探动态规划算法.html
Copyright Notice: All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Gynamic Programming