题目描述
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
示例 2:
输入: “cbbd”
输出: “bb”
解题思路
解析
我们目标是得到一个字符串的最长回文子串,假设字符串S=“axbacabyd”(x,y表示未知字符),则可以定义出最优子结构,假设字符串子串 bacab是回文子串,则当前字符串的最长回文子串有如下两种最优子结构:
- 若x == y,则最长回文子串为xbacaby
- 若x != y,则最长回文子串为bacab
通过题目可知边界条件为
- 字符串为单个字符时,此时最长回文子串为自身
- 字符串为两个字符时,若两个字符相等,则最长回文子串为自身,否则不存在最长回文子串
数学建模
定义 F(i , j) 为如下,
- 若 F(i , j) = true , Si…Sj是回文子串
- 若 F(i , j) = false, 其他情况
基于 F(i , j) 定义,可通过解析得到数学模型,即状态转移方程:
F(i , j) = true(F(i + 1, j -1) == true && S[i] == S[j])
F(i , j) = false (F(i + 1, j -1) == false || S[i] != S[j])
F(i , i) = true
F(i , i + 1) = true (S[i] == S[i + 1])
动态规划实现
接下来使用一个简单的例子,利用上述的数据建模,把求解最长回文子串的过程通过表格形式展示出来。
假设一个字符串str = “abcacfa”,回文子串求解过程如下:
-
当下标为i=j=0时,F(0 ,0) = true ,遂标为T;当下标为i=0,j=1时,此时 F(0 , 1) = false(S[0] != S[1]) ,遂标为F; 当下标为i=j=1时, F(1 , 1) = true ,遂标为T;当下标为i=0,j=2时, F(0 , 2) = false (F(1 , 1 ) == true && str[0] != str[2]) ,遂标为F; 当下标为i=1,j=2时,此时 F(1 , 2) = false(S[1] != S[2]) ,遂标为F,当下标为i=j=2时, F(2 , 2) = true ,遂标为T

-
根据第一步的方法 ,可以补全整个表格如下,补全上半部分即可,i=2, j =4 与 i = 4, j =2表达的是同一个子串,可得到最长回文子串的cac。
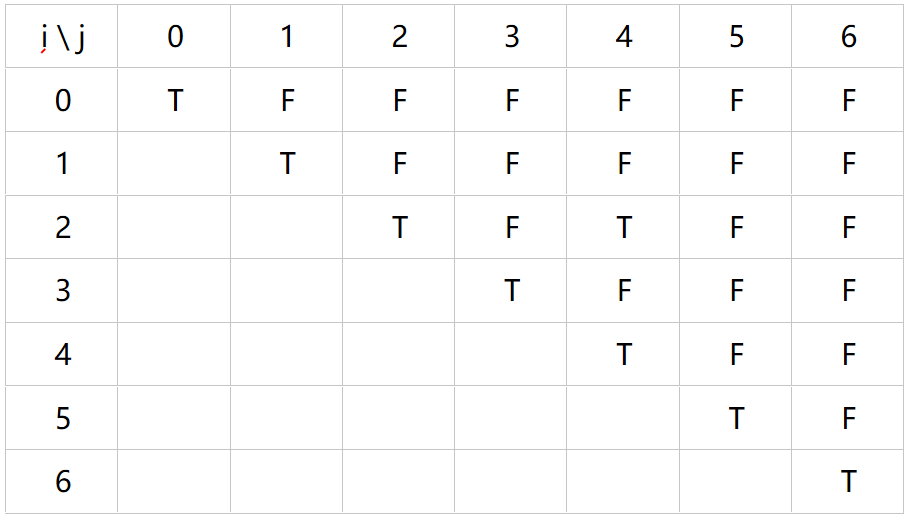
-
通过完整表格可知,要判断一个i,j范围的子串是否是回文子串,只需判断 (F(i + 1) == true && str[i] == str[j]) 是否为true即可,如下面红色所示。我们在进行代码编写时,也只需要保存上一次的计算结果即可。
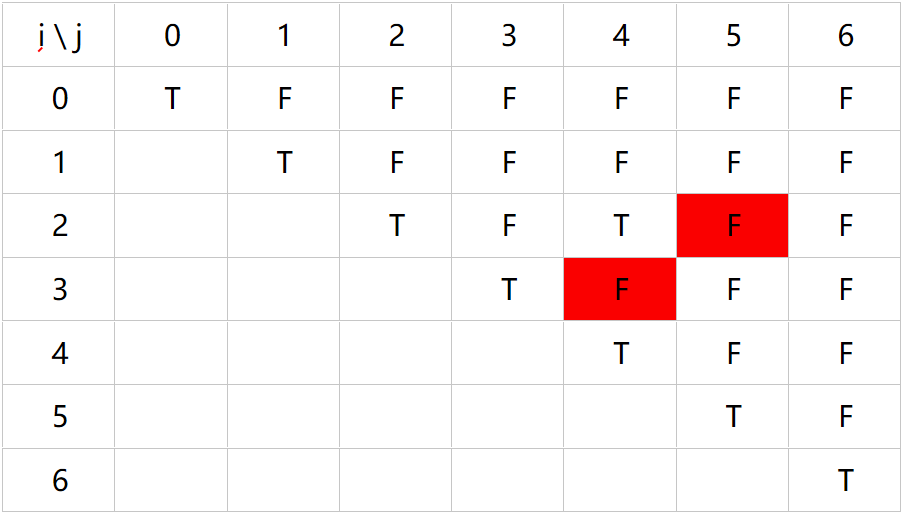
-
代码实现
public String getLongPalindromicSubstring(String str){ |
注:
- 时间复杂度:O(n^2)
空间复杂度:O(n) - 注释的代码是用TreeMap存储已知的回文子串(treeMap能根据键的自然顺序进行排序),直接取最后一个key-value返回即可。但是需要花费额外的空间来存储,为了效率问题,采用了start,end来记录当前最长回文子串,虽然多了很多行代码,但是效率得到了一定的提高。
- 挖个小坑 - 中心扩散算法求解,有时间来填 /(ㄒoㄒ)/~~
