重新认识时间复杂度

大O符号表示法

我们假设计算机运行一行基础代码需要执行一次运算。

int aFunc(void){
    printf("Hello,World!\n");  //需要执行1次
    return 0;  //需要执行1次
}

那么上面这段代码执行的总运算次数为2次。

int aFunc(int n){
    for(int i=0;i<n;i++){  //需要执行(n+1)次, 从0 -> n
        printf("Hello,World!\n");  //需要执行n次
    }
    return 0;//需要执行1次
}

上面的代码执行的总次数为 n + 1 + n + 1次。
使用 T(n) 来表示算法需要执行的总的运算次数，T(n) 为一个关于输入次数n的函数。例如上面的两段代码中：第一段代码 T(n) = 2；第二段代码 T(n) = 2n + 2。
但是仅仅有T(n) 是不够的，为了估算算法需要的运行时间和简化算法分析，再一次引入时间复杂度的概念。

定义：存在一个常数C和f(n)，使得当n >= C时，有T(n) <= f(n)，表示为T(n) = O(f(n))

就那T(n) = 2n 举例来说，存在C=2，且 n>=C时，总有f(n) = 2n+1 > T(n) = 2n，我们可以说说f(n)的增长速度是大于或等于T(n)的，也就是说f(n)为T(n)的上界，我们就可以用f(n)的增长速度来度量T(n)的增长速度，可以表示为 T(n) = O(f(n)) = O(2n + 1)，所以我们可以说这个算法的时间复杂度为O(f(n)) = O(2n+1)，O(f(n))表示运行算法所需要执行的指令数和f(n)成正比，n表示数据规模。
这个f(n) 并不是用来真实代表算法的执行时间的，它是用来表示代码执行时间随着输入n的增大的增长变化趋势，所以常数1 和与n相乘的常数2 对增长速度的影响不明显，所以可以省略，所以时间复杂度可以简化为 O(n)。

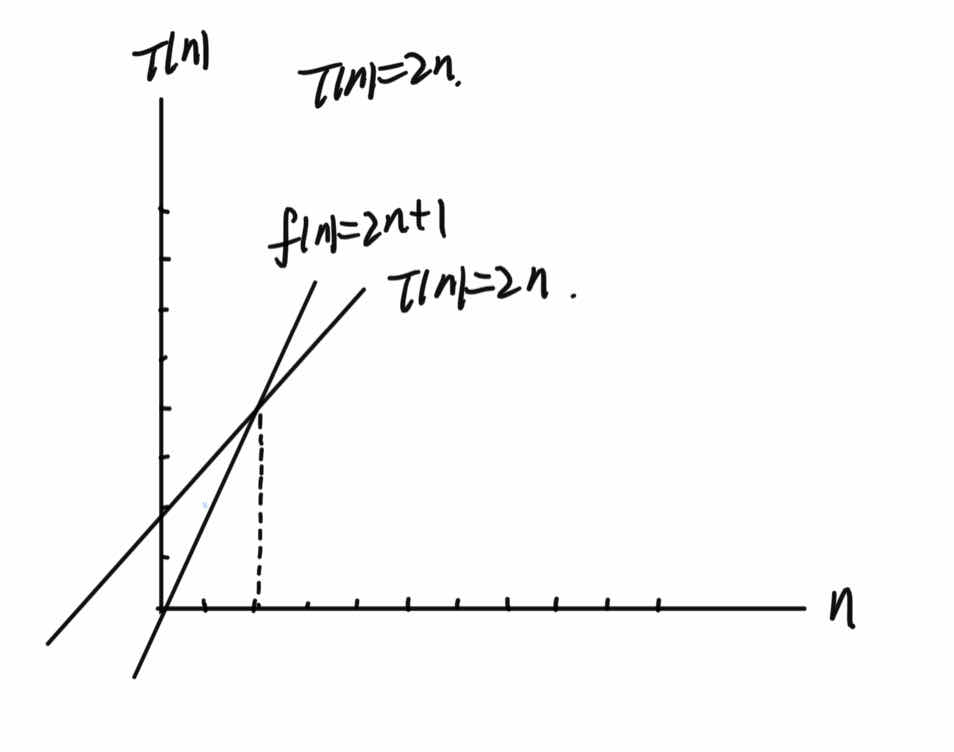
显然T(n) = O(f(n)) = O(3n+1)，T(n) = O(f(n)) = O(n^2)…… 都是成立，但是T(n) = O(f(n)) = O(2n+1)的增长速度相比其他是更加接近的，所以选择了它。
上面所提到的T(n) = O(f(n)) 也称为"大O符号表示法"。
下面可以用一个图来展示时间复杂度随着输入n的增大的增长变化趋势。从下图可知，常数对于时间复杂度的决定性总是微乎其微的，并且描述了一个事实，当数据规模n到达了某个零界点之后，时间复杂度低的算法的执行效率一定比时间复杂度高的执行效率更高。

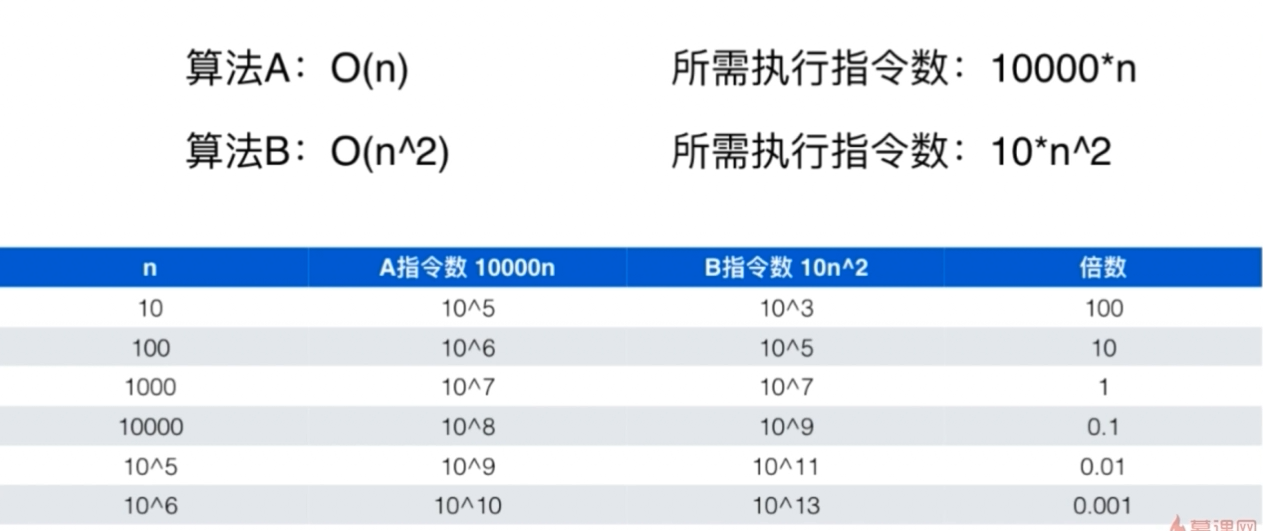
时间复杂度推导规律

推导T(n)
1. 对于一个循环，假设循环体的运算执行次数为 n ，循环次数为 m，则这个循环的总执行次数为 T(n) = n * m。
2. 对于多个循环，假设循环体的运算执行次数为 n，各个循环的循环次数分别是a，b， c…，则这个循环的总执行次数为T(n) = n * a * b * c…。分析的时候应该由里向外分析这些循环。
3. 对于顺序执行的语句或者算法，总的运算执行次数等于其中最大的运算执行次数。
4. 对于条件执行的语句或者算法，总的运算执行次数等于其中路径中最大的运算执行次数。
  综合说：从内向外进行分析，如果遇到函数调用，进行调用函数进行分析。
T(n) -> O(f(n))
假设我们已经得到了T(N)，即一个算法的执行次数，那么可以通过以下几个规律来简单推导：
1. 常数项对于函数增长速度的影响并不明显，忽略常数项。
  T(n) = c = O(1)，c为常数；
  T(n) = n + 1 = 1 = O(n)；
2. 高次项对于函数的增长速度的影响是最大的，保留最高次项，忽略低次项，若最高次项有常数相乘，忽略它；
  T(n) = n^3 + n^2 + n = O(n^3)；
  T(n) = 3 n^3 = O(n^3)；
  Ps：忽略低次项只适合于规模n属于同一个的情况。若某个时间复杂度为O(logn + m)，n和m属于两个不同的数据规模，则不可忽略其他任何一部分。

综合说：如果一个算法的执行次数是 T(n)，那么只保留最高次项，同时忽略最高项的系数后得到函数 f(n)，此时算法的时间复杂度就是 O(f(n))。

时间复杂度实例

O(1)时间复杂度实例

void swap(int a, int b) {
    int temp = a;
    a = b;
    b = temp;
}

O(n)时间复杂度实例

int sum(int n) {
    int result = 0;
    for(int i = 0; i <= n; i++) 
        result += i;
        return result;
    }
    
void reverse(String s) {
    int n = s.length();
    for(int i = 0; i < n / 2; i++)
        swap(s.charAt(i), s.charAt(n - 1 - i));
}

O(n^2)时间复杂度实例

void selectionSort(int[] arr, int n) {
    for(int i = 0; i < n; i++) {
            int minIndex = i;
        for(int j = i + 1; j < n; j++) {
            if(arr[j] < arr[minIndex])
                minIndex = j;
        }
        swap(arr[i], arr[minIndex]);
    }
}

内层if语句的执行次数为 (n - 1) + (n - 2) + (n - 3) …. + 0 = (0 + n - 1) * n / 2 => O(n^2)。

O(logn)时间复杂度实例

int binarySearch(int[] arr, int n, int target) {
    int l = 0, r = n - 1;
    while(l <= r) {
        int mid = l + (r - l) / 2;
        if (arr[mid] == target) return mid;
        if (arr[mid] > target) r = mid - 1;
        else l = mid + 1;
    }
    return -1;
}

① 在n个元素中查找
② 在 n / 2个元素中查找
③ 在 n / 4 个元素中查找
…….
④ 在1个元素中查找
n经过几次"除以2"操作后，等于1？ log(2)n = O(logn)
也可以这样计算，设操作次数为t，则 2^t <= n，t = log(2)n，得出为 O(logn)。

String intToString(int num) {
    String s = "";
    while(num > 0) {
        s += "0" + num % 10;
        num /= 10;
    }
    s = reverse(s);
    return s;
}

n经过几次"除以10"操作后，等于1？ log(10)n = O(logn)
为什么log(10)n和 log(2)n 的时间复杂度都可以视为O(logn)呢？主要是因为对数换底公式：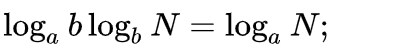

所以具体对数底是如何并不重要。

O(nlogn)时间复杂度实例

void hello (int n) {
    for(int sz = 1; sz < n; sz += sz)
        for(int i = 1; i < n; i++) 
            System.out.println("hello world");
}

O(sqrt(n))时间复杂度实例

boolean isPrime(int n) {
    for(int x = 2; x * x <= n; x++) {
        if(n % x == 0)
        return false;
    }
    return true;
}

X初始化为2，每次增加1，直到遍历到sqrt(n)就退出循环。

递归调用时间复杂度实例

int binarySearch(int[] arr, int l, int r, int target) {
    if(l > r){
        return -1;
        int mid = l + (r - l)/2;
        if (arr[mid] == target)
            return mid;
        else if (arr[mid] > target) 
            return binarySearch(arr, l, mid - 1, target);
        else 
            return binarySearch(arr, mid + 1, r, target);
    }
}

在每一个递归调用中，最多只进行一次递归调用，这时我们需要计算中递归调用的最大深度是多少，由实例4可知，由n->1，递归的最大深度为logn，则时间复杂度为O(logn)。
总结如下：如果在递归函数中，只进行一次递归调用，递归深度为depth，在每个递归函数中，时间复杂度为T，则总体的时间复杂度为O(T*depth)。

int f(int n) {
    assert(n >= 0);
    if (n == 0)
        return 1;
    return f(n - 1) + f(n - 1);
}

在每一个递归调用中，会进行两次递归调用，此时应该更加关注的是计算调用的次数，通常可以通过画递归树的方式来计算调用次数。时间复杂度为O(2^n)。

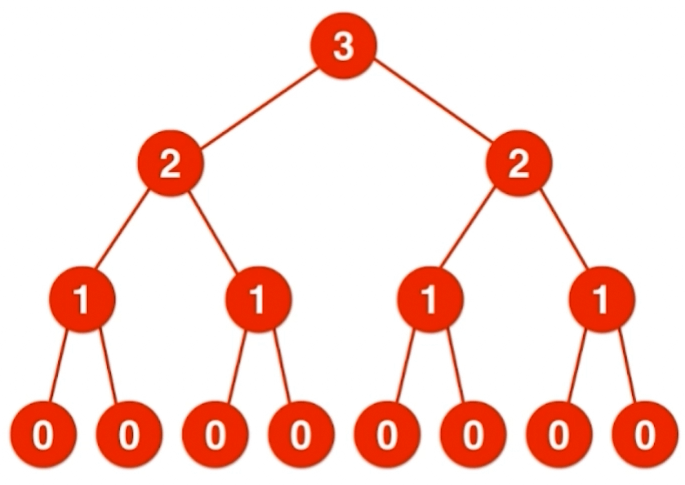
递归树层数为4，2^0 + 2^1+ 2^2 + 2^3 = 2^n -1 =15

均摊复杂度分析实例

例如对于Java中ArrayList数组，它是一个动态数组，此类的动态数组在每个的插入操作为O(1)的时间复杂度，但是当超过当前数组容量时会进行数组扩容操作，扩容操作的时间复杂度为O(n)，但是就算在插入操作中存在着O(n)时间复杂度的扩容操作，也不能够说插入操作的时间复杂度为O(n)，它仍然是O(1)的时间复杂度，因为O(n)时间复杂度的扩容操作均摊到了前面n次的O(1)操作之中了。

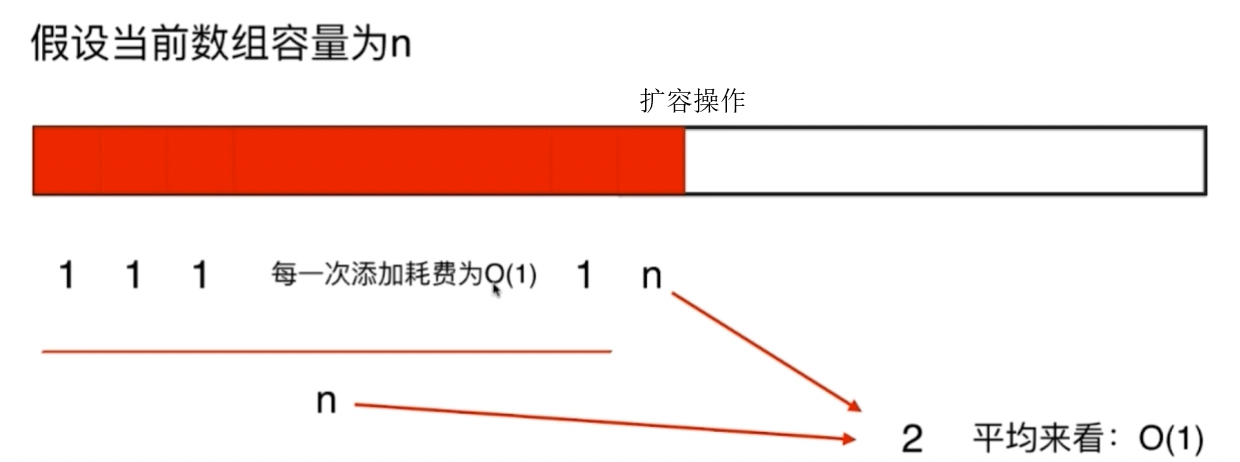
每个的删除操作为O(1)的时间复杂度，那么假设当剩余元素为当前数组容量的一半时会进行数组缩小操作，那么此时也可以使用如上所说明的均摊复杂度分析。

但是如上可能会存在复杂度震荡问题，即当在数据扩容和缩小的零界点交替进行添加和删除操作会使得时间复杂度退化为O(n)。
有一个字符串数组，将数组中的每一个字符串按照字母序排序；之后再将整个字符数组按照字典序排序，整个操作的时间复杂为？
解析：
假设最长的字符串长度为s；整个数组中有n个字符串。
对每个字符串排序时间复杂度为O(slogs)，将数组中的每一个字符串按照字母序排序：O(nslogs)，将整个字符串数组按照字典序排序：O(snlogn)，其中snlogn为排序所需要的比较次数。
综上所述，整个时间复杂度为：O(nslogs) + O(snlogn) = O(nslogs + snlogn) =
O(ns(logs + logn))

扩展

"O"是渐进上界符号（Big-oh - 欧米可荣），用它评估算法的复杂度得到的只是问题规模充分大时的一个上界，但是这个定义是严格的学术定义，按照该定义来说，归并排序算法的时间复杂度是O(nlogn)，并且是O(n^2)，这种说法是正确的，因为O(n^2)也是满足条件的一个上界。但是通常来讲，我们使用"O"来表示算法执行的最低上界。
下图展示了不同时间复杂度随着数据规模n的增长的所需要执行指令数的增长速度。
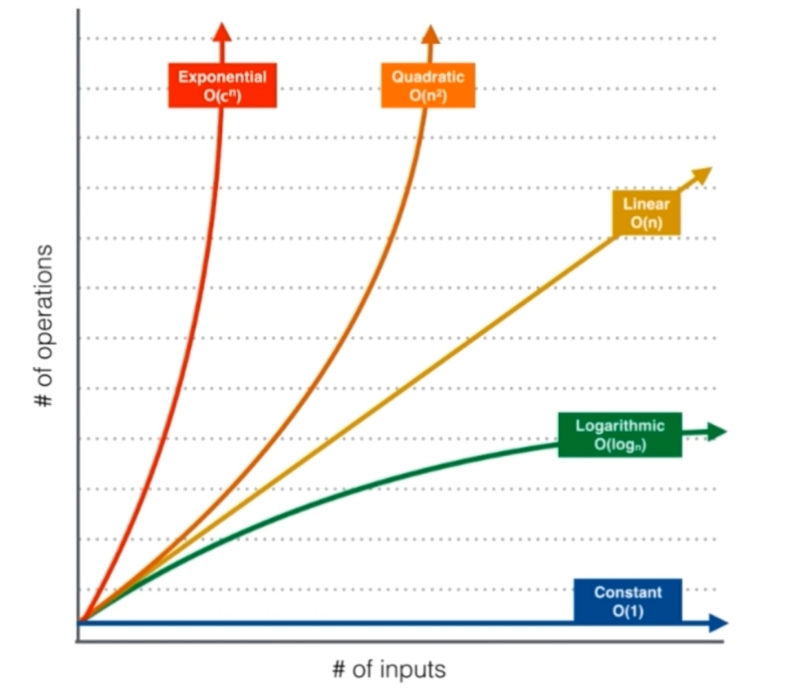
数据规模的概念
如果想要在1s之内解决问题：
O(n^2) 的算法可以处理大约10^4级别的数据；
O(n)的算法可以处理大约10^8级别的数据；
O(nlogn)的算法可以处理大约10^7级别的数据。
空间复杂度
多开一个辅助数据：O(n)；多开一个辅助的二维数组：O(n^2)；多开常数空间：O(1)；递归调用具有空间代价

参考链接

[1] https://www.jianshu.com/p/f4cca5ce055a
[2] https://blog.csdn.net/so_geili/article/details/53353593
[3] https://coding.imooc.com/class/chapter/82.html